Visualizing the Hindu divisibility test

Posted on November 11, 2018 by mAnasa-taraMgiNI

Prologue
This article continues on the themes covered by the last two (here and here) relating to factorization and the primitive root modulo of a prime number. Early in ones education one learns the divisibility tests for the first few primes: 2, 3, and 5. Of these divisibility by 2 and 5 is trivial. Divisibility by 3 is also easily achieved: e.g. Is 771 divisible by 3? 7+7+1=15; \; 1+5=6. We see that the successive addition of digits reduces the original number to 6 which is divisible by 3; hence, the original number is divisible by 3. Of course, division by 3 is not a big deal; yet, for big numbers this is an easy method for mentally determining divisibility.

Beyond these three simple cases, in our school days we determined the divisibility by other primes using brute force — by dividing the test number by the given prime. When we reached college, a gentleman of great mathematical ability asked us if we could think of a generalization of the divisibility test for 3 for other primes. Seeing that we were unable to do so, he proceeded to tell us of such a method. He then mentioned that he had learned this via Suryanarayana of Vishakhapatnam who possessed enormous mathematical knowledge and capacity. Suryanarayana had further informed him that it was a folk Hindu method that was known in South India. Shortly thereafter, we saw the same method with some tricks for quick implementation in the pre-computer age described by the late Śaṃkarācarya Bhāratī Kṛṣṇa Tīrtha-jī (hereinafter SBKT) of the Govardhana pīṭha in his curious mathematical work with 16 foundational sūtra-s. He called the method veṣṭana, which he rendered in English as osculation, and presented it as an example of his sūtra: “ekādhikeṇa pūrveṇa |”

The Hindu divisibility test
The procedure goes thus:
1) Let p be a prime other than 2, 3, 5 for which divisibility is already accounted for. Let the test number be n_0 which is written as n_0=10a_0+b_0.
2) Find the first number (10c-1) \mod p =0, i.e. the first multiple of p which is of the form 10c-1. Thus, this number will necessarily be of the form 10d+9, where c=d+1. That is how it relates to SBKT’s “ekādhikeṇa pūrveṇa |”
3) This c is termed the veṣṭaka or ‘osculator’ for the procedure. We then compute n_1=a_0+b_0c.
4) We again write n_1=10a_1+b_1 and repeat this procedure: n_2= a_1+b_1c.
5) If p divides n_0 then this procedure terminates in a small and easily recognized multiple of p. Any further application of the above procedure on that number yields the same number.

Let us illustrate it with an example: Is n_0=3249 divisible by p=19?
For p=19, 2 \times 10 -1=19\; \therefore c=2. Now we use the osculator c=2 for applying the above procedure.
We get 324+9 \times 2=342; \; 34+2\times 2= 38; \; 3+8\times 2=19
We reach 19 indicating that 3249 is divisible by 19. Applying the above procedure to 19 yields 19 again. Indicating that it is a terminal number of the process. In a practical application from the pre-computer age we don’t have to go all the way: we could stop for e.g. at 38, which we recognize as a multiple of 19. Further, for bigger numbers SBKT gives certain tricks which would be useful in such pre-computer applications.

What if a number is not divisible by p? As an example consider the case: Is n_0=178 divisible by 19? Of course, in this case the answer is quite obvious; nevertheless, it allows us to illustrate what happens if we apply the above procedure on it. We get the following sequence of n_j, j=0, 1, 2 ...:
178\rightarrow 33 \rightarrow (9 \rightarrow 18 \rightarrow 17 \rightarrow 15 \rightarrow 11\rightarrow 3 \rightarrow 6 \rightarrow 12 \rightarrow 5 \rightarrow 10 \rightarrow 1\rightarrow 2 \rightarrow 4 \rightarrow 8 \rightarrow 16 \rightarrow 13 \rightarrow 7 \rightarrow14 ) \rightarrow9
We observe that, unlike the divisible n_0 which converges to a single number, the non-divisible n_0 after the first 2 terms enters a repeating cycle of 18 terms. Again, for practical purposes if one just wanted to test divisibility one obtains the answer much earlier.

The basic divisibility graphs
We can do this divisibility procedure for several successive n_0, say for all n_0=1..200 and p=19, and the illustrate the conglomerate results as an ordered graph (Figure 1). The graph’s nodes are the numbers n_j obtained while applying the above divisibility procedure until we hit a cycle or converge. The edges indicate which number leads to which, with the relative thickness indicating the frequency with which they occur for this range of n_0 (scaled by hyperbolic arcsine).

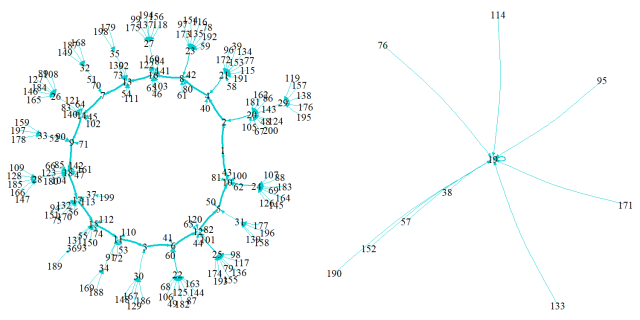
Tirtha_div_Fig1Figure 1

One also notices that all n_0 in this range, which are divisible by 19, directly converge to it. The remaining numbers converge directly or indirectly by different paths to a central directed ring R_1 with components r_1, r_2, r_3.... These are the same as the terms of the cycle obtained in the above example. One also notices that in this example the ring size S(R_1)=18, i.e. number of terms in the ring, corresponds to cycle length of the decimal expansion of \tfrac{1}{19} or j=18 when 10^j \mod 19=1 for the first time. This j, in this case 18, is known as the multiplicative order of 10 (\mod p), which was shown by Carl Gauss to correspond to the cycle of the decimal expansion of \tfrac{1}{p} . The terms of this ring R_1 includes all the number from 1..18. Thus, it is also obvious that the sum of the terms of in ring R_1 is divisible by p:

\displaystyle \left(\sum_{j=1}^{S(R_1)} r_j \right) \mod p =0

To further explore these patterns, we next consider the case of p=13 and plot the same for graph for n_0=1..200 in Figure 2.

Tirtha_div_Fig2Figure 2

We observe that all n_0 divisible by 13 in this range converge to 3 terminal nodes: 13, 26 and 39. The remaining n_0 converge directly or indirectly to one of 6 rings with 6 terms each. i.e. S(R_{1..6})=6. Here again we notice that the size of these rings is the same as the multiplicative order of 10\mod 13 (j=6 when 10^j \mod 13=1 for the first time), which is cycle length of the decimal expansion of of \tfrac{1}{13}. Further, together the 6 rings include all numbers from 1..38 barring 13 and 26 which are divisible by 13. It is easy to see that \sum_{j=1}^{38} j-13-26 is divisible by 13. However, we also notice that the sum of the terms of each of the six rings is also divisible by 13:

\displaystyle \left(\sum_{j=1}^{S(R_k)} r_{kj} \right) \mod p =0; \; k=1..6

We next consider the case of p=7 and n_0=1..200 (Figure 3).

Tirtha_div_Fig3Figure 3

In this graph the numbers divisible by 7 converge to 2 endpoints either 7 itself or 49 (when they are multiples of 49). All the remaining numbers directly or indirectly converge to a large ring with 42 terms, which includes all numbers from 1..48 except for 7, 14, 21, 28, 35, 42. Thus, it is easy to see that the sum of the terms of this ring will be divisible by 7. Further, the multiplicative order of 10 \mod 7 is 6. Thus, the number of terms in the ring is multiple of that 42=6 \times 7.

To sum up, we may note the following features of these divisibility graphs:
1) The residue system of p=19 for base 10 (till 10^j \mod p for j=1,2,3... produces 1 as the residue for the first time, i.e. till j is equal to the multiplicative order) is: 10, 5, 12, 6, 3, 11, 15, 17, 18, 9, 14, 7, 13, 16, 8, 4, 2, 1. The base 10 residue system for p=13 is: 10, 9, 12, 3, 4, 1. The base 10 residue system of p=7 is: 3, 2, 6, 4, 5, 1. We observe that the penultimate residue in each case is what SBKT calls the “osculator” c used in the divisibility test.

2) Looking the graphs, it becomes clear that the non-divisible n_0 converge to one or more directed rings, the sizes of which are either the multiplicative order m for base 10 or a multiple of m. A number n is a primitive root of p if the residue system of n^j, j=1,2,3...p-1 contains all numbers from 1..p-1. If 10 is not a primitive root of the p , the divisibility by which we are testing, then we will necessarily have multiple rings. If 10 is a primitive root of p we can in some cases get a single ring with its terms being all numbers from 1..p-1 (e.g. 19). Alternatively, we can get a large single ring whose size can be some multiple of the multiplicative order (e.g. p=7) or multiple rings whose sizes are different multiples of the multiplicative order (e.g. p=17).

Tirtha_div_Fig4Figure 4. Divisibility graph for p=17

3) The terms included in all the rings of convergence taken together for a given p range from 1..10c-2, where c is the penultimate residue of the system and the osculator. Of course, all numbers divisible by p in this range are excluded from the rings as they are nodes of separate components of the graph that converge to single root, an integer divisible by p. Thus, for p=13, the osculator is c=4. So, the integers covered in the rings would be from 1 to 38, with 13 and 26 not being in the rings. For p=7, the osculator c=5; hence, the ring would cover the integers from 1 to 48, with 7, 14, 21, 28, 35, 42 being excluded. When p=17, the osculator is c=12. Thus, the rings will extend from 1 to 118, with 17, 34, 51, 68, 85, 102 being excluded.

4) From the above it is obvious that the sum of the numbers in all the rings taken together would be divisible by p. The less obvious feature is that the sum of the numbers in each individual ring of the convergence graph is also divisible by p. Thus, the numbers are placed in each ring in such a way that two constraints are simultaneously met, namely: 1)that of divisibility of the sum of the numbers in each ring by p and 2) that of each ring size being a multiple of the base 10 multiplicative order modulo the given p. In the case of p=13 placing the numbers in 6 separate rings can satisfy the above constraints for each ring. In the case of p=17 placing them in 3 separate rings can satisfy them, while in the case of p=7 they need to be in a single large ring to meet the constraints.

5) An obvious but structurally distinctive feature of the divisibility graph is that 1 can never be reached directly from any n_0 unless it is a member of the ring to which 1 belongs. From the procedure it is clear that it can be reached only from 10. 10 is the first number in the base 10 residue system for any p>7 and will necessarily be part of the ring. Further, in whichever ring 1 occurs, by the nature of the procedure, it would always lead next to the osculator c as the next node in the ring. c always comes just before it in the residue system for base 10 (e.g. for 13: 10, 9, 12, 3, 4, 1): thus 10\rightarrow 1 \rightarrow c is fixed a motif in the divisibility ring reverse order of their occurrence in the residue system. The longest path of the divisibility graph ending in a ring always passes through this c (However, there could be graphs with multiple equally long paths passing through other ring nodes in certain cases like p=17).

One wonders is an encryption system along the lines of the Diffie-Hellman-Merkle mechanism can be made using these divisibility graphs.

The reduced divisibility graphs
The above-described graphs were based on the simple divisibility method found in folk Hindu mathematics and SBKT’s mathematical exposition. However, for practical purposes SBKT gives an additional step, which he terms the “casting out of the primes”. This goes thus: We again write the test number as n_0=10a_0+b_0. We then obtain n_1= a_0+(b_0c \mod p), where c is the osculator as above. Thus, we first reduce b_0c to its residue modulo the p, the divisibility by which we are testing, before adding it to a_0 to arrive at n_1.

As a numerical example let us consider testing the divisibility of 99 by 7. The osculator for 7 is c=5. Thus 9 \times 5=45. We now take 45 \mod 7= 3 and use it in place of 45. Thus, we get n_1=12 which allows us to decide on the matter of divisibility right away. However, we could continue the procedure to convergence, as we did above, in order to compute the convergence graphs for different p. In this case we observe the following:
1) If 10 is a primitive root of p then we get a bipartite graph: One component derived from all the non-divisible n_0 has a central ring, which has as its terms all numbers from 1..p-1. The other component is a tree graph converging to p which includes all the n_0 divisible by p. Examples of this are the graphs for p=7 or p=17

Tirtha_div_Fig5Figure 5. The convergence graph for p=7

Tirtha_div_Fig6Figure 6. The convergence graph for p=17

2) If 10 is not a primitive root of p then we get a multipartite graph. One component, as above, is a tree graph converging on p and includes all the n_0 divisible by p. The remaining components have central rings whose size is the multiplicative order m of 10 \mod p. The number of these ring components is \tfrac{p-1}{m}. Here again, the sum of the numbers in each ring is divisible by p. Together they include all integers from 1..p-1. Examples of this are the graphs for p=13 and p=41.

Tirtha_div_Fig7Figure 7. The convergence graph for p=13. Here m=6 for base 10; thus we get \tfrac{13-1}{6}=2 components with central rings.

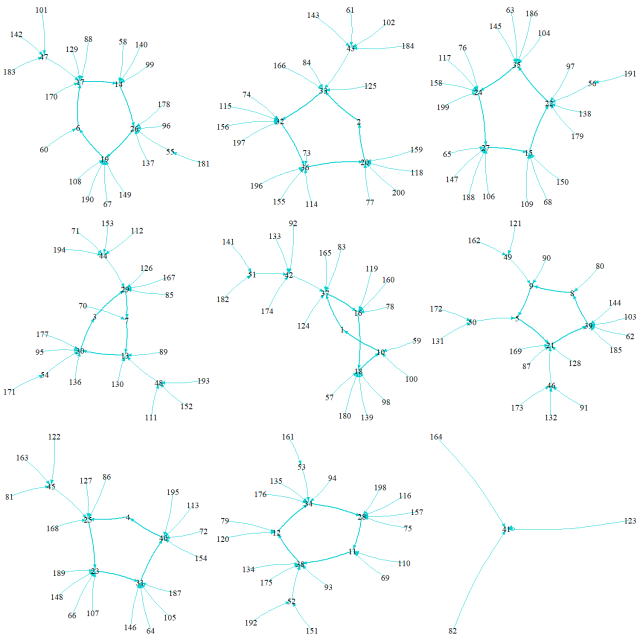Tirtha_div_Fig8Figure 8. The convergence graph for p=41. Here m=5 for base 10; thus we get \tfrac{41-1}{5}=8 components with central rings.

In these graphs too the longest path terminating in a ring passes through the osculator c, which is reached from 1 on the ring. Here again, 1 is reached from 10, the first residue of the residue system for base 10 \mod p for all primes p>7. However, given that 10 \mod 7 =3, for p=7, 1 is reached from 3 in the ring. In conclusion, this version of the divisibility graph makes apparent the close relationship it has to the period of the decimal form of the fraction \tfrac{1}{p}, which we considered in the previous article.

This entry was posted in Scientific ramblings and tagged , , , , , , . Bookmark the permalink.